¿Cómo se representa geométricamente la Adición y Sustracción de Vectores en R3?

Para representar geométricamente la suma y resta de vectores en R3 se pueden usar el método del paralelogramo y el del triángulo, pero ya que estos métodos los toque en el post anterior, dejare a continuación un link con un vídeo donde podremos apreciar como funcionan ambos métodos correctamente:

¿Que es Adición y Sustracción de Vectores en R3?

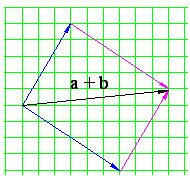
Para sumar o restar vectores se suman o se restan sus respectivos componentes. Para realizar esto existe el método del paralelogramo el cual consiste en colocar los vectores de forma en que sus orígenes coincidan haciendo que los otros dos lados del paralelogramo sean las paralelas que conforman al mismo
.

También existe otro método en el que se colocan ambos vectores y luego se une el origen con el extremo, haciendo que este tenga una forma de triángulo

¿Cómo calcular la Dirección y el Sentido de un Vector en R3?

La dirección de un vector esta definida por la medida que tienen los ángulos del mismo, estos se calculan a partir de sus cosenos los cuales equivalen a X,Y y Z entre la magnitud o módulo del vector ( ||v|| = √ (x² +y² +z²), una vez se tiene el coseno se despeja el ángulo (Alpha, Beta y Gamma) y se calcula, dando como resultado la dirección


En el vídeo que dejó a continuación se puede apreciar como se define la dirección de un vector en R3:

Conclusión

El vector tiene un significado mucho mas grande de lo que creemos, de hecho, conocer los vectores nos ayuda a entender los fenómenos naturales que ocurren en el universo, es decir, que podemos aplicar los vectores en nuestra vida cotidiana.
Cuando hablamos de vectores en R3 hablamos sobre un espacio tridimensional, entonces los vectores también se pueden aplicar en el espacio tridimensional en donde vivimos. El espacio tiene elementos como la anchura, la altura y la profundidad por lo tanto los vectores nos sirven para definir un punto en el mismo, es decir, que los vectores nos ayudan a describir matemáticamente el espacio en el que vivimos

¿Donde se utilizan los vectores en R3?

Por ejemplo, cuando caminamos, describimos sumas de vectores en los que los vectores son sumas de distancias con cierta dirección y sentido, al andar en un automóvil, las distintas velocidades a las que andamos son distintos vectores, al adelantar otro automóvil, debes hacer mentalmente una resta de vectores, en los cuales los vectores son las velocidades que llevan los automóviles con su correspondiente dirección y sentido, al abrir una puerta vemos sumas de vectores, primero para girar la manilla, luego para abrirla. A fin de cuentas, cualquier cosa a la cual le puedas asignar un número o una magnitud y a la vez asignarle una dirección (y un sentido) es un vector.

Para mas ejemplos de donde se pueden utilizar vectores, pueden consultarlos en el vídeo que dejare a continuación:

¿Cuales son los Octantes?

En R3 hay un total de 8 octantes:
Primer Octante: P(X,Y,Z)
Segundo Octante: P(-X,Y,Z)
Tercer Octante: P(-X,-Y,Z)
Cuarto Octante: P(X,-Y,Z)
Quinto Octante: P(X,Y,-Z)
Sexto Octante: P(-X,Y,-Z)
Séptimo Octante: P(-X,-Y,-Z)
Octavo Octante: P(X,-Y,-Z)

Podemos apreciar los 8 octantes en el vídeo que dejo a continuación:

¿Como graficar en R3?

En el vídeo que dejo a continuación podemos apreciar el método para graficar en R3:

¿Cuales son los elementos de un vector?

• Módulo: Es la longitud o medida de un vector (Desde el inicio hasta el final), y siempre es positivo
• Dirección: Se le llama dirección de un vector, a la dirección de la recta que lo contiene.
• Sentido: Dos vectores que tienen la misma dirección pueden tener igual o diferente sentido dependiendo del signo que se le aplique al vector, ya sea positivo o negativo.

¿Que son vectores en R3?

Teniendo conocimiento de que el vector es un segmento de recta que se cuenta a partir de un punto en el espacio, un vector en R3 se puede determinar como un vector el cual se cuenta a partir de un punto de un espacio tridimensional, es decir, que se le puede dar al vector características tridimensionales y este se puede mover en el espacio, en los ejes X, Y y Z.

¿Que es un Vector?

Un vector fijo del plano es un segmento cuyos extremos están dados en un orden (segmento orientado). Se representa como AB (con una flecha en la parte superior) siendo A y B los extremos. Los puntos en que comienza y termina el vector se llaman origen y extremo, respectivamente.

¿Que significa R3?

Se denomina R3 a un espacio vectorial tridimensional, es decir, que es un espacio el cual cuenta con tres planos mutuamente perpendiculares. Estos tres planos se forman a partir de 3 rectas perpendiculares entre sí las cuales se interceptan en un punto de origen denotado como "0". A estas rectas se les conoce por el nombre de ejes de coordenada y se designan como eje X, Y y Z.
Se considera que los ejes X y Y están en un plano horizontal, y el eje Z en un plano vertical.